「思维+构造」”蔚来杯”2022牛客暑期多校训练营6 I. Line

题面传送门

题意：给定含有n个向量的向量集，请构造一个点集，满足对于点集内的所有点，在任何向量集里的向量方向的直线上有且只有d个点存在（包括自己）。

考虑n=2的情况。

比如d=3，可以容易构造出下图：

发现其实是对于一维情况下往向量方向平移。
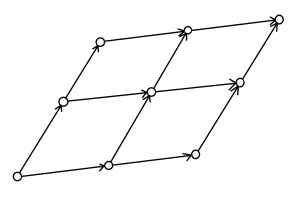
在上图的情况下拓展到n=3：

总结：构造过程就是不断向新向量方向对已加入点集的点平移。

为了不让点集中的点在平移时和之前的向量冲突，平移的距离要逐渐增大，这里采用23的幂次。

#include <bits/stdc++.h>
using namespace std;
namespace IO{
    #define I inline
    I char tc(){static char tr[10000],*A=tr,*B=tr;return A==B&&(B=(A=tr)+fread(tr,1,10000,stdin),A==B)?EOF:*A++;}
    I void read(int &x){
        char c;int y=1;x=0;
        while(((c=tc())<'0'||c>'9')&&c!='-');c=='-'?y=-1:x=c-'0';
        while((c=tc())>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0';
        x*=y;
    }
    // I void read(int &x){scanf("%d",&x);}
    #undef I
}using namespace IO;

int gcd(int x,int y){return !y?x:gcd(y,x%y);}

const int Base = 23;

int n,d,Rev[10],Cnt;
set<pair<int,int> >A;
vector<pair<int,int> >Ans;

int main()
{
    read(n),read(d),Rev[0]=1;
    for(int i=1;i<=6;++i)Rev[i]=Rev[i-1]*Base;
    for(int i=1,x,y,t;i<=n;++i){
        read(x),read(y),t=gcd(x,y);
        A.insert(make_pair(x/t,y/t));
    }
    Ans.push_back(make_pair(0,0));
    for(auto p:A){
        ++Cnt;
        for(int i=0,m=Ans.size();i<m;++i){
            for(int j=1;j<d;++j)
                Ans.push_back(make_pair(Ans[i].first+j*p.first*Rev[Cnt],Ans[i].second+j*p.second*Rev[Cnt]));
        }
    }
    printf("%d\n",Ans.size());
    for(auto p:Ans)printf("%d %d\n",p.first,p.second);
}