题目链接
题意:给定一棵n个点的树,有q次操作,每次修改一个点的点权,或者询问以x为根时,所有节点子树点权和的平方和。
首先考虑如果没有换根操作时(以1为根),如何处理点权修改。
对于修改一个点的点权,可以看出增加或减少两者的差值。
修改一个点的点权只会对它和它到1点路径上的子树点权和有影响。(路径维护)
考虑用树链剖分维护,树上问题转换为序列问题,用线段树维护区间平方和。
设序列值si,即每个点的子树点权和,那么:
\Sigma (s_i+p)^2 = \Sigma (s_i^2 + 2*s_i*p + p*p) = \Sigma s_i^2 + \Sigma (2*s_i*p + p*p)
在线段树上维护普通值和平方值即可。(PS:PushDown的时候先更新平方值)
然后想想怎么换根。
我们可以在log2n的时间内求出以1为根的答案(Ans0),假设我们需要把根换到x。
同样的,换根只会对它和它到1点路径上的子树点权和有影响。
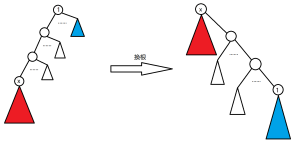
记路径点集为D,son i表示i点在链上的儿子。
删去原树路径上点的影响后加上换根树路径上的点影响,可知:
Ans = Ans0 - \sum_{i\in D}s_i^2 + \sum_{i\in D,i\neq x }(s_1 - s_{son_i})^2 + s_1^2
化简式子得:
Ans = Ans0 - \sum_{i\in D}s_i^2 + |D|s_1^2-2s_1\sum_{i\in D,i\neq 1}s_i+\sum_{i\in D,i\neq 1}s_i^2 \\\quad\quad\ \ = Ans0 + (|D|-1)s_1^2-2s_1\sum_{i\in D,i\neq 1}s_i
维护路径和即可。
#include <bits/stdc++.h>
using namespace std;
namespace IO{
#define I inline
I char tc(){static char tr[10000],*A=tr,*B=tr;return A==B&&(B=(A=tr)+fread(tr,1,10000,stdin),A==B)?EOF:*A++;}
I void read(int &x){
char c;int y=1;x=0;
while(((c=tc())<'0'||c>'9')&&c!='-');c=='-'?y=-1:x=c-'0';
while((c=tc())>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0';
x*=y;
}
// I void read(int &x){scanf("%d",&x);}
#undef I
}using namespace IO;
class TreeChainSubdivision{
#define N 200005
typedef long long LL;
private:
int n,root;
int head[N],nxt[N<<1],to[N<<1],Cnt;
int dep[N],fa[N],siz[N],hvson[N];
int id[N],idcnt,na[N],top[N];
LL Seg[N<<2],Seg2[N<<2],lazy[N<<2];
void update(int Node){
Seg[Node]=Seg[Node<<1]+Seg[Node<<1|1];
Seg2[Node]=Seg2[Node<<1]+Seg2[Node<<1|1];
}
void PushDown(int Node,int L,int R){
if(!lazy[Node])return ;
lazy[Node<<1]+=lazy[Node];
lazy[Node<<1|1]+=lazy[Node];
Seg2[Node<<1]+=2ll*lazy[Node]*Seg[Node<<1]+1ll*lazy[Node]*lazy[Node]*L;
Seg2[Node<<1|1]+=2ll*lazy[Node]*Seg[Node<<1|1]+1ll*lazy[Node]*lazy[Node]*R;
Seg[Node<<1]+=lazy[Node]*L;
Seg[Node<<1|1]+=lazy[Node]*R;
lazy[Node]=0;
}
void Build(int Node,int L,int R){
if(L==R)return (void)(Seg[Node]=na[L],Seg2[Node]=na[L]*na[L]);
int Mid=L+R>>1;
Build(Node<<1,L,Mid);
Build(Node<<1|1,Mid+1,R);
update(Node);
return ;
}
LL QuerySection(int Node,int L,int R,int Ql,int Qr){
if(L>R)return 0;
if(Ql<=L&&R<=Qr)return Seg[Node];
int Mid=L+R>>1;
LL res=0;
PushDown(Node,Mid-L+1,R-Mid);
if(Mid>=Ql)res+=QuerySection(Node<<1,L,Mid,Ql,Qr);
if(Mid< Qr)res+=QuerySection(Node<<1|1,Mid+1,R,Ql,Qr);
update(Node);
return res;
}
LL QuerySection2(int Node,int L,int R,int Ql,int Qr){
if(L>R)return 0;
if(Ql<=L&&R<=Qr)return Seg2[Node];
int Mid=L+R>>1;
LL res=0;
PushDown(Node,Mid-L+1,R-Mid);
if(Mid>=Ql)res+=QuerySection2(Node<<1,L,Mid,Ql,Qr);
if(Mid< Qr)res+=QuerySection2(Node<<1|1,Mid+1,R,Ql,Qr);
update(Node);
return res;
}
void ModifySection(int Node,int L,int R,int Ml,int Mr,int v){
if(L>R)return ;
if(Ml<=L&&R<=Mr){
lazy[Node]+=v;
Seg2[Node]+=2ll*v*Seg[Node]+1ll*v*v*(R-L+1);
Seg[Node]+=1ll*v*(R-L+1);
return ;
}
int Mid=L+R>>1;
PushDown(Node,Mid-L+1,R-Mid);
if(Mid>=Ml)ModifySection(Node<<1,L,Mid,Ml,Mr,v);
if(Mid< Mr)ModifySection(Node<<1|1,Mid+1,R,Ml,Mr,v);
update(Node);
return ;
}
void dfs1(int x,int f,int deep){//处理出每个节点的深度、父节点、子树大小和重儿子
dep[x]=deep,fa[x]=f,siz[x]=1;
int mxsiz=0;
for(int i=head[x];~i;i=nxt[i])if(to[i]^f){
dfs1(to[i],x,deep+1);
siz[x]+=siz[to[i]];
a[x]+=a[to[i]];
if(mxsiz<siz[to[i]])mxsiz=siz[to[i]],hvson[x]=to[i];
}
}
void dfs2(int x,int Ltop){//按dfs序标号、处理每条链,Ltop表示链的顶端
id[x]=++idcnt;
na[idcnt]=a[x];
top[x]=Ltop;
if(!hvson[x])return ;
dfs2(hvson[x],Ltop);
for(int i=head[x];~i;i=nxt[i])if(to[i]^hvson[x]&&to[i]^fa[x]){
dfs2(to[i],to[i]);
}
}
public:
int a[N];
void init(int _n,int _root){//初始化函数,n点数,root树根
n=_n,root=_root;
Cnt=idcnt=0;
memset(head,-1,sizeof(head));
}
void AddEdge(int u,int v){//前向星加边
nxt[Cnt]=head[u],to[Cnt]=v,head[u]=Cnt++;
}
void Solve(void){//主体函数
dfs1(root,0,1),dfs2(root,root),Build(1,1,n);
}
LL QueryRoute(int x,int y){//查询两点路径信息
LL res=0;
while(top[x]^top[y]){//x、y不在一条链上
if(dep[top[x]]<dep[top[y]])swap(x,y);//让x所在链作为深度更深的点
res+=QuerySection(1,1,n,id[top[x]],id[x]);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
res+=QuerySection(1,1,n,id[x],id[y]);
return res;
}
LL QueryRouteS(int x){//查询两点路径信息
LL res=0;
while(top[x]^top[1]){//x、y不在一条链上
res+=QuerySection(1,1,n,id[top[x]],id[x]);
x=fa[top[x]];
}
res+=QuerySection(1,1,n,id[1]+1,id[x]);
return res;
}
void ModifyRoute(int x,int y,int c){//维护两点路径信息
while(top[x]^top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
ModifySection(1,1,n,id[top[x]],id[x],c);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
ModifySection(1,1,n,id[x],id[y],c);
}
LL QuerySubtree(int x){//查询子树信息
return QuerySection(1,1,n,id[x],id[x]+siz[x]-1);
}
LL QuerySubtree2(int x){//查询子树信息
return QuerySection2(1,1,n,id[x],id[x]+siz[x]-1);
}
void ModifySubtree(int x,int c){//修改子树信息
return (void)(ModifySection(1,1,n,id[x],id[x]+siz[x]-1,c));
}
int GetDep(int x){
return dep[x];
}
#undef N
}T;
const int N = 2e5+5;
int n,Q,_a[N];
int main()
{
read(n),read(Q);
T.init(n,1);
for(int i=1,x,y;i<n;++i){
read(x),read(y);
T.AddEdge(x,y),T.AddEdge(y,x);
}
for(int i=1;i<=n;++i)read(T.a[i]),_a[i]=T.a[i];
T.Solve();
for(int Opt,x,y;Q;--Q){
read(Opt);
if(Opt==1){
read(x),read(y);
T.ModifyRoute(1,x,y-_a[x]);
_a[x]=y;
}
else{
read(x);
int pc=T.QueryRoute(1,1);
printf("%lld\n",T.QuerySubtree2(1)+1ll*(T.GetDep(x)-1)*pc*pc-2ll*pc*T.QueryRouteS(x));
}
}
}
