A. Min Max Swap

题意：有两个数组a和b，可以做任意次操作，将两数组某一位置交换，求两数组各自最大值乘积的最小值。

容易发现，两数组中所有数的最大值是一定要用的，所以我们选择最大数存在的那个数组，然后将其他位置上较大的数都放到最大数的数组中，这样另一个数组中的最大数就会尽量小。

注意可能存在相同大小的最大数。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 105
using namespace std;

int T,n,a[MAXN],b[MAXN],_a[MAXN],_b[MAXN];

int main()
{
    for(scanf("%d\n",&T);T;--T){
        scanf("%d",&n);int Mx=0,o1=0,o2=0,y=0,ans=2e9;
        for(int i=1;i<=n;++i)scanf("%d",&a[i]),_a[i]=a[i];
        for(int i=1;i<=n;++i)scanf("%d",&b[i]),_b[i]=b[i];
        for(int i=1;i<=n;++i)Mx=max(Mx,max(a[i],b[i]));
        for(int i=1;i<=n;++i){
            if(Mx==a[i])o1=1;
            if(Mx==b[i])o2=1;
        }
        if(o1){
            for(int i=1;i<=n;++i)
                if(a[i]<b[i])swap(a[i],b[i]);
            for(int i=1;i<=n;++i)y=max(y,b[i]);
            ans=min(ans,Mx*y);
            for(int i=1;i<=n;++i)a[i]=_a[i],b[i]=_b[i];
        }
        if(o2){
            for(int i=1;i<=n;++i)
                if(a[i]>b[i])swap(a[i],b[i]);
            for(int i=1;i<=n;++i)y=max(y,a[i]);
            ans=min(ans,Mx*y);
            for(int i=1;i<=n;++i)a[i]=_a[i],b[i]=_b[i];
        }
        printf("%d\n",ans);
    }
}

B. Fun with Even Subarrays

题意：给定一个数组a，可以做这样的操作，选择l和k，将a_{l+k}至a_{l+2k-1}覆盖到a_{l}至a_{l+k-1}上，问最少做几次操作能够使整个数组的数一样。

容易发现，一定要将后面部分覆盖到前面部分，也就是可知最后一个数是一定要用的。

所以不断地往前覆盖，理论上最多只要logn次就可以，但要注意，在向前覆盖时，每次结束后，要向前拓展最左区间，因为可能有和最后一个值相等。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 200005
using namespace std;

int T,n,a[MAXN];

int main()
{
    for(scanf("%d",&T);T;--T){
        scanf("%d",&n);int dis=n,ans=0,ds=1;
        for(int i=1;i<=n;++i)scanf("%d",&a[i]);
        for(int i=n;i;--i)if(a[i]!=a[i-1]){
            dis=i;break;
        }
        while(dis>1){
            dis-=n-dis+1;
            ++ans;
            while(dis>1&&a[dis-1]==a[n])--dis;
        }
        printf("%d\n",ans);
    }
}

C. And Matching

题意：给定一个存在n个数\{0~n-1\}的集合，和一个数k，让你判断是否能够满足:\Sigma_{i=1}^{n/2} a_i\&\ b_i =k，如果满足输出每一对a_i和b_i，否则输出-1。同时a_i和b_i都是集合中的数，且集合中的数只能使用一次。

容易发现，当n-1不等于k时，可以将n-1与k配对，与n-1-k配对，剩下的两两配对消去，这样就构成了k这个答案。

但是当n-1=k时，考虑如何构成答案。

发现可以由n-1和n-2先构成n-2，即二进制下最后一位为，但是我们相当于需要构造一个1，所以我们想到用n-3和1进行配对，但是这样原来应当和n-1、n-3配对的0、2没人配对了，那么将他们配对起来，对答案没有影响，剩下的两两配对。容易发现，这个方法当且仅当n>4(n>=8)时可以实现，所以当且仅当n=4,k=3时输出-1。

Tips：n-1不等于k时，注意判断配对时i是否等于n-1-k或k，且k=0要特别判断。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

int T,n,k;

int main()
{
    for(scanf("%d",&T);T;--T){
        scanf("%d%d",&n,&k);
        if(n-1!=k){
            printf("%d %d\n",0,n-1-k);
            for(int i=1;i<n>>1;++i)if(i!=n-1-k&&i!=k)printf("%d %d\n",i,n-1-i);
            if(k)printf("%d %d\n",k,n-1);
        }       
        else {
            if(n==4)puts("-1");
            else{
                for(int i=3;i<n/2;++i)printf("%d %d\n",i,n-i-1);
                printf("%d %d\n%d %d\n%d %d\n",n-1,n-2,n-3,1,0,2);
            }
        }
    }
}

D. Range and Partition

题意：给定一个存在n个数且数的范围在[ 1,n]的数组，试确实一个值域[x,y]使得该数组可以分为k部分，且每一部分在范围内的数都严格比在范围外的数多，求最小的y-x。输出x和y，然后输出区间的划分。

可以发现，划分区间时，只要值域内的数比值域外的数多一即可，那么只要在值域内的数，比值域外的数总数多k个，那么这个值域就是对的，用桶来统计数的数量，同时我们用蠕虫法可以求得最小值域，然后根据值域来求区间，只要刚好多一即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 200005
using namespace std;

int T,n,k,a[MAXN],t[MAXN];
int main()
{
    for(scanf("%d",&T);T;--T){
        scanf("%d%d",&n,&k);
        int tot=0,Ans=2e9,_i,_j,l=1;
        for(int i=1;i<=n;++i)t[i]=0;
        for(int i=1;i<=n;++i)scanf("%d",&a[i]),++t[a[i]];
        for(int i=1,j=0;i<=n;++i){
            for(;tot<k+n-tot&&j<=n;)tot+=t[++j];
            if(j>n)break;
            if(Ans>j-i+1)_i=i,_j=j,Ans=j-i+1;
            tot-=t[i];
        }
        printf("%d %d\n",_i,_j);
        tot=0;
        for(int i=1;i<=n;++i){
            if(k==1){
                printf("%d %d\n",l,n);
                break; 
            }
            tot+=(a[i]>=_i&&a[i]<=_j?1:-1);
            if(tot==1)
                printf("%d %d\n",l,i),l=i+1,--k,tot=0;
        }
    }
}

E. Paint the Middle

题意：给定数组a，和一个全为的数组c，可以进行这样的操作：每次选三个数a_i,a_j,a_k,i< j< k,且满足a_i=a_k,c_i=c_j=c_k=0，然后将c_j变为1，问\Sigma_{i=1}^n c_i的最大值

贪心。

考虑相同数一定是最左最右两数之间全部赋值成1，可以理解为一个类似区间覆盖问题，处理两端点的数，都赋值为1。

从前向后枚举，遇到未赋值的点，比较记录的已经赋值点的数值最右端，选择较远的边界赋值。

这种方法为什么行得通？看以下贪心方法。

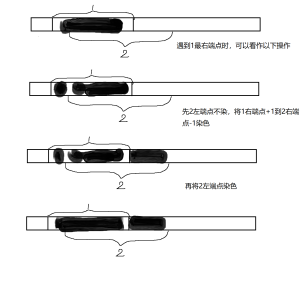
相当于白嫖了一段染色，且距离更远。

#include <bits/stdc++.h>
#define MAXN 200005
using namespace std;
int T,n,ans,ls,a[MAXN],Right[MAXN],vis[MAXN];

void Solve(int l,int r){
    if(l>r)return;
    ans+=r-l+1;
    for(int i=l;i<=r;++i)vis[i]=1;
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i)scanf("%d",&a[i]),Right[a[i]]=i;
    for(int i=1;i<=n;++i)
        if(vis[i]==0){
            if(Right[a[ls]]>=Right[a[i]])Solve(i+1,Right[a[ls]]-1);
            else Solve(i+1,Right[a[i]]-1);
            ls=0;
        }
        else
            if(Right[a[ls]]<Right[a[i]])ls=i;
    printf("%d",ans);
}

F. Flipping Range

题意：给定数组a和集合B，可以对a按B中数字大小对连续区间取负，问\Sigma_{i=1}^n a_i的最大值。

可以发现，B中数字相互组合，相当于做gcd，那么最优解就是B的gcd值，即最短区间翻转长度。

同时，对于最短长度，移动一位，相当于隔这个长度翻转，此时相当于取出L+k,2*L+k...这些下标的数组，用翻转区间长度为2来求最优解。

且发现翻转区间为2可以转化为任意两数翻转。

如果这些取出的数存在，那么一定能够将所有数转为正数。

不存在的情况就要根据负数的数量奇偶性判断。

原因是由于其实翻转操作依然是由k区间翻转构成，所以要判断前k个元素每一个的翻转奇偶性来存储到不同的数组中。
下面是代码作者原话。

So if all chains have odd negative numbers, you can use operations to make all except the last k(k is the gcd of all lengths) elements positive. Then you can use one operation to make the last k elements positive.
My idea is that you can use two operations to flip two numbers whose distance is actually k, and one operation can be interpreted as one operation in the last k elements and several pair flip operation. So the only thing that need to enumerate is the parity of the flip operation done to the last k elements, which is represented as the separation of sum[0] and sum[1].

我的想法是，你可以使用两个操作来翻转两个距离实际上是k的数字，一个操作可以被解释为最后k个元素中的一个操作和几个对翻转操作。因此，唯一需要枚举的是对最后k个元素执行的翻转操作的奇偶性，它表示为sum[0]和sum[1]的分离。因此，如果所有链都有奇数负数，可以使用运算使除最后k（k是所有长度的gcd）元素外的所有元素都为正。然后你可以使用一个操作使最后的k个元素为正。

//By ABitstOCHASTIC, contest: Codeforces Round #768 (Div. 1), problem: (D) Flipping Range
#include<bits/stdc++.h>
using namespace std;

#define int long long
int N , A[1000003] , T , M;

signed main(){
    ios::sync_with_stdio(0);
    for(cin >> T ; T ; --T){
        cin >> N >> M; for(int i = 1 ; i <= N ; ++i) cin >> A[i];
        int L = 0 , x; for(int i = 1 ; i <= M ; ++i){cin >> x; L = __gcd(L , x);}
        int sum[2] = {0,0};
        for(int i = 1 ; i <= L ; ++i){
            int als = 0 , sign = 1 , mn = 1e9;
            for(int j = i ; j <= N ; j += L){
                als += abs(A[j]); sign *= A[j] ? abs(A[j]) / A[j] : 0;
                mn = min(mn , abs(A[j]));
            }
            sum[0] += als - 2 * (sign == -1) * mn;
            sum[1] += als - 2 * (sign == 1) * mn;
        }
        cout << max(sum[0] , sum[1]) << endl;
    }
    return 0;
}