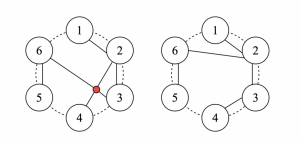
题意:给定在环上按顺时针从小到大的一个n排列,并给出每个点的度的奇偶性,求是否能构造一棵树,且树边在圆内不交叉(如下图例,左交叉为不符合方案),若存在,输出该树n-1条边
首先是判断无法构造的情况,很容易想到一棵树(无向图)的出入度总和一定为偶数(一条边提供两个度),所以奇数度的点不为偶数个则为无法构造。
下面是构造策略:考虑奇度数之间的偶度数点,容易想到将它们串起来来构造偶度数,但此时串起后两端仍有两个度数,这是应当将这两个度数分配给两个奇度数点。这个时候奇度数点的偶数个性质有用武之地了。
我们这么构造:将第一个奇度数点作为根,将其通过一条条偶数度数点的串与其他奇度数点连接,并使其它奇度数点的度只为1。例如:
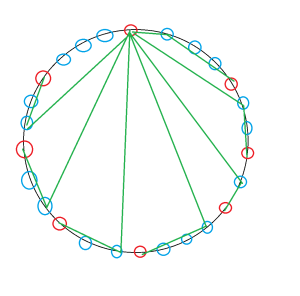
但是这么做以后发现第一个奇度数点左侧有一条未串起的偶度数点。进行改良:最后一个奇度数点先经过第一个奇度数点左侧的偶度数串后再按原来策略连接。
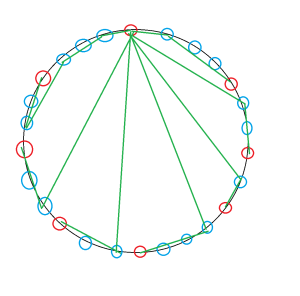
如此,一个完美的构造方法就完成了。(欣赏一下找到的一篇比较简洁的代码)
//By cp152, contest: Codeforces Round #793 (Div. 2), problem: (D) Circular Spanning Tree
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int t,n;
char b[200005];
int s,e;
int num;
int main()
{
scanf("%d",&t);
while(t--)
{
num=s=e=0;
scanf("%d",&n);
scanf("%s",b+1);
for(int i=1;i<=n;i++) if(b[i]^'0') s=s?s:i,e=i,++num;
if(num&&num%2==0)
{
cout<<"YES\n";
bool bb=1;
int l=s;
for(int i=s+1;i<e;i++)
{
if(bb)
{
cout<<l<<' '<<i<<'\n';
l=i;
}
else
{
cout<<i<<' '<<i-1<<'\n';
}
if(b[i]^'0')
{
bb=!bb;
}
}
for(int i=s-1;i>=1;i--)
{
cout<<l<<' '<<i<<'\n';
l=i;
}
for(int i=n;i>=e;i--)
{
cout<<l<<' '<<i<<'\n';
l=i;
}
}
else
{
cout<<"NO\n";
}
}
return 0;
}