模式串、主串与KMP、trie和AC自动机
模式串、主串与KMP、trie和AC自动机

模式串、主串与KMP、trie和AC自动机

Ⅰ 模式串与主串

一、字符串匹配问题与BF算法

所谓字符串匹配，实际上就是询问：字符串P是否为字符串S的子串？若是，则P出现在S的哪些位置？

由此问题其实可以得到一个非常简单的算法：BF算法。

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力算法。

二、模式串和主串

在字符串匹配问题中，字符串P也被称为模式串，字符串S也被称为主串。

也就是字符串匹配问题可以这样阐述：给定模式串和主串，主串中存在或多处存在模式串，存在则求出模式串位置。

Ⅱ KMP算法

一、BF的不足

当我们的BF算法遇到这样的情况时，会导致复杂度急剧退化：

BF算法在遇到上述情况时，对于每一位都会进行匹配，导致复杂度退化到上界O(nm)。

二、KMP算法

1. KMP的重匹配机制

KMP算法的核心是失配后的重匹配机制。

发明KMP的三位学者，Knuth，Morris和Pratt，就这样想：如果字符串在失配时不是将模式串向后移动一格，而是保持匹配的位置，将模式串向后移动很多格呢？看下面这个例子（红框处失配）：

当在模式串上匹配时，到达第5个字符，我们可以这样移动模式串：

可以看出，每次失配后，能够保留的是前缀与当前后缀一致的最长长度。

以下下标均记从0开始。

若最长一致前后缀长度为k，则有：P[0~k]==P[j-k-1~j-1]

2. next数组

我们记next[i]为模式串i位置前的最长一致前后缀（不包括i），亦可以理解为在i位置处失配后应该移动模式串到哪。

next数组有这样的性质：P[0~next[i]-1]==P[i-next[i]~i-1]。

如果我们预先知道了模式串next数组的值，那么我们可以很快地对主串进行匹配，复杂度是O(n+m)的（具体放在后面说明）。

那么如何求next数组呢？这也是KMP算法最为精髓的地方：模式串的自匹配。

看下面这张图，假设我们已经求得了next[1~i-1]，且i一开始等于0，而next[0]=-1, j=-1，j表示与以i结尾的字符串后缀相共同的最长前缀。

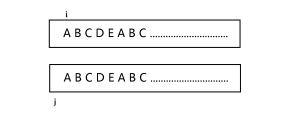
自匹配过程中其实只有三种情况：

  1. 起始位置无法自匹配，也就是刚刚开始匹配的情况和匹配途中完全失配的情况；

  2. 当前两点位置相匹配；

  3. 当前两点位置失配，且j存在可前置的next。

1和2情况其实是一致处理的，因为1中情况可以理解为-1位置处匹配。

3情况就是将j移为next[j]，也算是利用了自身的性质。

那么在自匹配的过程中，每次失配都是向前找到最大的共同前后缀来继续匹配，从而能保证next数组的性质。

int* GetNext(char* S){
    int j=0,k=-1,n=strlen(S);
    int *next=(int*)malloc(n*sizeof(int));
    next[0]=-1;
    while (j<n-1) {
       if(k==-1 || S[j]==S[k])next[++j]=++k;
       else k=next[k];
    }
    return next;
}

3. 主串匹配

得到模式串的next数组后，模式串对于主串的匹配就显得那么简单了。

n=strlen(s1),m=strlen(s2);
for(int i=0,j=0;i<n;){
    if(j<0||s1[i]==s2[j])++i,++j;
    else j=nxt[j];
    if(j==m)printf("%d\n",i-m+1),j=nxt[j];//输出所有能相匹配的起始点位置
}

Ⅲ Trie

一、定义

字典树(trie)，顾名思义，一颗像字典一样的树。

又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

如百度百科定义中所言，Trie是一种利用公共前缀来减少查询时间的数据结构。

例如下图：


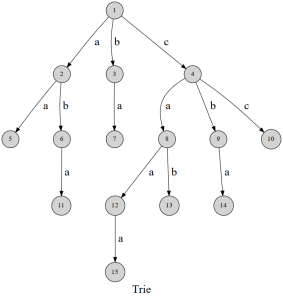
Trie的每一个叶节点都代表了一个字符串，其为从根节点到叶节点路径上所有的字符顺序拼接。

二、实现

Trie树中每一个节点都至多有26个指针，指向当前点对应之后的字符；同时有一个布尔类型，用于判断是否有一个字符串在当前节点处结尾（或者用int类型存储结尾的数量，甚至同时可以在Trie树上维护子树信息）。下面代码简单用数组实现。

const int N = 1e5 + 10;
int son[N][26];  // 存储树中每个节点的子节点
int cnt[N];      // 存储以每个节点结尾的单词数量
int Rcnt;        // 0号点既是根节点，又是空节点
char str[N];
void insert(char *str) {//插入字符串
    int p = 0;
    for (int i=0; str[i]; i++) {
        int u=str[i]-'a';
        if (!son[p][u])son[p][u]=++Rcnt;  // 如果 p 不存在孩子 u, 则创建
        p = son[p][u];
    }
    cnt[p]++;
}

int query(char *str) {//查询字符串数量
    int p = 0;
    for (int i=0; str[i]; i++) {
        int u str[i]-'a';
        if(!son[p][u])return 0;
        p=son[p][u];
    }
    return cnt[p];
}

三、0-1 Trie

0-1 Trie是一种Trie的变体，一般用于维护一些二进制下的数的属性。

比如维护异或极值。

给你一棵带边权的树，求(u,v) 使得u 到v 的路径上的边权异或和最大，输出这个最大值。点数不超过10^5，边权在 (0,2^{31})内。

首先DFS出每一个节点到根的路径上的异或值，记为xor[u]。

可以知道两点的路径边权异或和xor(u,v)=xor[u]^xor[v]（因为他们的LCA以上的xor值会自己抵消）。

那么将n个点的xor插入到0-1 Trie中去。

对于每一个xor[u]，在0-1 Trie中查询一遍，方法如下：

  1. 如果存在与当前xor[u]位置不同的，如当前位xor[u]为0，0-1 Trie上当前位存在1，那么就反方向走。

  2. 如果不存在，就同方向走。

最终到达根节点的路径即为当前xor[u]的最大边权异或和，然后对于每一个xor都做一遍，即可得到最终答案。

下面代码摘自OI Wiki。

#include <algorithm>
#include <cstdio>
using namespace std;

const int N = 100010;

int head[N], nxt[N << 1], to[N << 1], weight[N << 1], cnt;
int n, dis[N], ch[N << 5][2], tot = 1, ans;

void insert(int x) {
  for (int i = 30, u = 1; i >= 0; --i) {
    int c = ((x >> i) & 1);  // 二进制一位一位向下取
    if (!ch[u][c]) ch[u][c] = ++tot;
    u = ch[u][c];
  }
}

void get(int x) {
  int res = 0;
  for (int i = 30, u = 1; i >= 0; --i) {
    int c = ((x >> i) & 1);
    if (ch[u][c ^ 1]) {  // 如果能向和当前位不同的子树走，就向那边走
      u = ch[u][c ^ 1];
      res |= (1 << i);
    } else
      u = ch[u][c];
  }
  ans = max(ans, res);  // 更新答案
}

void add(int u, int v, int w) {  // 建边
  nxt[++cnt] = head[u];
  head[u] = cnt;
  to[cnt] = v;
  weight[cnt] = w;
}

void dfs(int u, int fa) {
  insert(dis[u]);
  get(dis[u]);
  for (int i = head[u]; i; i = nxt[i]) {  // 遍历子节点
    int v = to[i];
    if (v == fa) continue;
    dis[v] = dis[u] ^ weight[i];
    dfs(v, u);
  }
}

int main() {
  scanf("%d", &n);

  for (int i = 1; i < n; ++i) {
    int u, v, w;
    scanf("%d%d%d", &u, &v, &w);
    add(u, v, w);  // 双向边
    add(v, u, w);
  }

  dfs(1, 0);
  printf("%d", ans);
  return 0;
}

Ⅳ AC自动机

一、确定有限状态自动机(DFA)

一个确定有限状态自动机由以下五个部分组成：

  1. 字符集（\Sigma），该自动机只能输入这些字符。

  2. 状态集合（Q）。如果把一个DFA 看成一张有向图，那么DFA 中的状态就相当于图上的顶点。

  3. 起始状态（start），start\inQ，是一个特殊的状态。起始状态一般用 s表示，为了避免混淆，本文中使用 start。

  4. 接受状态集合（F），F\subseteqQ，是一组特殊的状态。

  5. 转移函数（\delta），\delta 是一个接受两个参数返回一个值的函数，其中第一个参数和返回值都是一个状态，第二个参数是字符集中的一个字符。如果把一个DFA 看成一张有向图，那么DFA中的转移函数就相当于顶点间的边，而每条边上都有一个字符。

AC自动机其实就是一种DFA。

二、AC自动机

AC自动机其实是一种以Trie为骨架，KMP为筋脉的自动机。

AC自动机一般用于多模式串下的主串匹配，你可以将KMP看作AC自动机的特殊情况。

那么当然了，AC自动机的第一步就是建立一棵模式串的Trie树。

建立完成后，我们要对这棵Trie树构建fail失配指针。

三、fail指针的构建

和KMP算法的next数组类似，fail指针其实构建只有三种情况：

假设当前节点u，其父节点p，指向u的字符指针为c。

  1. 如果 trie[fail[p],c]存在：则让u的fail指针指向trie[fail[p],c]。

  2. 如果 trie[fail[p],c]不存在：那么我们继续找到trie[fail[fail[p]],c]。重复 1 的判断过程，一直跳fail指针直到根结点。

  3. 如果真的没有，就让fail指针指向根结点。

但是，与KMP不同的是，由于模式串数量众多，fail指针指向所有模式串的前缀(Trie树上的节点)中匹配当前状态的最长后缀，也就是u与fail[u]的后缀一致。

void build() {
    for(int i=0;i<26;i++)
        if(tr[0][i])q.push(tr[0][i]);
    while (q.size()) {
        int u = q.front();
        q.pop();
        for(int i=0;i<26;i++) {
            if (tr[u][i])
                fail[tr[u][i]]=tr[fail[u]][i], q.push(tr[u][i]);
            else
                tr[u][i]=tr[fail[u]][i];//①
        }
    }
}

而且构建时有一个较巧妙的地方在于(①)，如果不存在下一个字符则视为失配，且将其连接到fail位置的trie[fail[u]][i]，如果仍然不存在，其实之前就已经完成了找到存在位置的工作，那么trie[fail[u]][i]指向的有可能是trie[fail[fail[u]]][i]，以此类推，这样能够节省我们找下一个匹配位置的时间。

四、查询

这里以查询共出现了多少个模式串为例。

int query(char *t) {
    int u=0,res=0;
    for(int i=1;t[i];i++) {
        u=tr[u][t[i]-'a'];  // 转移
        for (int j=u;j&&e[j]!=-1;j=fail[j]) {
            res += e[j],e[j]=-1;
        }
    }
    return res;
}

每一次经过Trie上不存在的节点时，都会通过构建fail指针时的①来舍弃一部分前缀使得保留的最低限度状态，从而满足正确完成匹配。

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注