A. Mark the Photographer
题意:给定2n个人,问是否能够排成前后两排,满足第一排的每一位上都小于第二排。
简单理解,就是一个贪心,先sort所有数,然后第i个数和第i+n个数匹配,然后判断一下可行性就可以了。
然鹅我题面没看清甚至WA了一发 🙁 。
#include <bits/stdc++.h>
using namespace std;
int T,n,x,a[1000];
int main()
{
for(scanf("%d",&T);T;--T){
scanf("%d%d",&n,&x);int res=1;
for(int i=1;i<=n<<1;++i)scanf("%d",&a[i]);
sort(a+1,a+(n<<1)+1);
for(int i=1;i<=n;++i)if(abs(a[i+n]-a[i])<x){
res=0;break;
}
puts(res?"YES":"NO");
}
}B. Mark the Dust Sweeper
题意:给定a数组,若区间[i,j]满足i+1 ~ j-1的数都严格大于0,那么可以将ai减一,aj加一,问将原数组a1~an-1清空最少需要多少次操作。
注意到其实对于那些0位置,需要额外花费1代价来走过这些点,因为我们只需要1代价使得整改区间右端+1(无论左端点是否有变化)。
所以总代价和其实就是第一个非0 ai后面0的个数加上\Sigma a_i。
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int T,n,x,a[N];
int main()
{
for(scanf("%d",&T);T;--T){
scanf("%d",&n);
long long res=0;
for(int i=1;i<=n;++i)scanf("%d",&a[i]);
for(int i=1;i<n;++i)res+=a[i];
for(int i=1;i<=n;++i)if(a[i]){
for(int j=i+1;j<n;++j)if(!a[j])++res;
break;
}
printf("%lld\n",res);
}
}C. Mark and His Unfinished Essay
题意:给定字符串S,c次操作,每次选择一个当前字符串的区间,将其加在字符串后面,形成新字符串;Q次询问最终字符串某一个位置上的字符。
对于每一个最终位置上的字符,它一定对应了某一个操作或者初始状态。
那么如果我们找到了那个状态,我们就可以通过操作所使用的区间来将查询的位置向前移动到另一个相等的点。
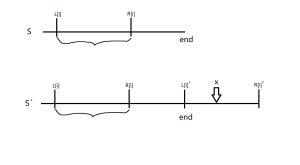
可以看出来,x在上一个操作中的位置为L+x-end-1。
记录每次操作完的字符串总长,每次找到第一个左端点比当前位置小的操作,更新新位置。
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int T,n,c,q,m;
long long l[45],r[45],ed[45];
char s[N];
int main()
{
for(scanf("%d",&T);T;--T){
scanf("%d%d%d\n",&n,&c,&q);
scanf("%s",s+1);
ed[0]=n;
for(int i=1;i<=c;++i){
scanf("%lld%lld",&l[i],&r[i]);
ed[i]=ed[i-1]+r[i]-l[i]+1;
}
for(long long x;q;--q){
scanf("%lld",&x);
for(int i=c;i;--i)if(ed[i-1]<x){
x=l[i]+x-ed[i-1]-1;//更新位置
}
printf("%c\n",s[x]);
}
}
}D. Mark and Lightbulbs
题意:给定两个01串AB,若A中一点i有S[i-1]!=S[i+1],那么可以将i点的0或1翻转,问A转换到B的最小操作数,无解输出-1。
考虑将原串看成一块一块的1,那么我们可以花费1单位的代价将区间的左或右端点增或减1。
那么处理出A和B中每一个1区间,然后ans就是每个对应的区间的左右端点差的绝对值和。
-1的情况就是两种,一种是最左或者最右端有不同的情况,和1区间数量不相等。
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int T,n,Cnt1,Cnt2;
char s1[N],s2[N];
struct Que{
int l,r;
}c1[N],c2[N];
int main()
{
for(scanf("%d",&T);T;--T){
Cnt1=Cnt2=0;
scanf("%d\n",&n);
scanf("%s",s1+1);
scanf("%s",s2+1);
if(s1[1]!=s2[1]||s1[n]!=s2[n]){
puts("-1");continue;
}
for(int i=1;i<=n;++i)if(s1[i]=='1'){
int j=i;
c1[++Cnt1].l=i;
for(;j<=n;++j)if(j<n&&s1[j+1]=='0')break;
c1[Cnt1].r=j;
i=j+1;
}
for(int i=1;i<=n;++i)if(s2[i]=='1'){
int j=i;
c2[++Cnt2].l=i;
for(;j<=n;++j)if(j<n&&s2[j+1]=='0')break;
c2[Cnt2].r=j;
i=j+1;
}
if(Cnt1!=Cnt2){
puts("-1");
continue;
}
long long ans=0;
for(int i=1;i<=Cnt1;++i){
ans+=abs(c1[i].l-c2[i].l)+abs(c1[i].r-c2[i].r);
}
printf("%lld\n",ans);
}
}E. Mark and Professor Koro
题意:给定a数组,每次操作可以选择两个相等的ai,删去后再加入一个新数ai + 1;q次询问,每次删去a[k],加入新数L,求对于当前的新数组来说,经过若干次操作的后的最大值。
容易想到的是,每次操作可以理解为2进制下的加法,那么我们就可以理解为用数据结构维护2进制下的"单"位加减法。
这题我用线段树维护,查询最近右端0或1点直接二分,总复杂度O(nlog^2n)。
比赛的时候找最近右端0或1nt了,不然应该调的出来。
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,q,a[N];
int Seg[N+17<<2],Seg2[N+17<<2],lazy[N+17<<2];
#define Lim (N+12)
void pushdown(int Node){
if(lazy[Node]<0)return ;
Seg[Node<<1]=Seg2[Node<<1]=lazy[Node];
Seg[Node<<1|1]=Seg2[Node<<1|1]=lazy[Node];
lazy[Node<<1]=lazy[Node<<1|1]=lazy[Node];
lazy[Node]=-1;
}
void update(int Node){
Seg[Node]=min(Seg[Node<<1],Seg[Node<<1|1]);
Seg2[Node]=max(Seg2[Node<<1],Seg2[Node<<1|1]);
}
int Get(int Node,int L,int R,int x){
if(L==R)return Seg[Node];
int Mid=L+R>>1;
pushdown(Node);
if(Mid>=x)return Get(Node<<1,L,Mid,x);
else return Get(Node<<1|1,Mid+1,R,x);
update(Node);
}
void insert(int Node,int L,int R,int x,int p){
if(L==R)return (void)(Seg[Node]=Seg2[Node]=p);
int Mid=L+R>>1;
pushdown(Node);
if(Mid>=x) insert(Node<<1,L,Mid,x,p);
else insert(Node<<1|1,Mid+1,R,x,p);
update(Node);
}
int Getmin(int Node,int L,int R,int gl,int gr){
if(L>R)return 2;
if(gl<=L&&R<=gr)return Seg[Node];
int Mid=L+R>>1,ans=2;
pushdown(Node);
if(Mid>=gl)ans=min(ans,Getmin(Node<<1,L,Mid,gl,gr));
if(Mid< gr)ans=min(ans,Getmin(Node<<1|1,Mid+1,R,gl,gr));
update(Node);
return ans;
}
int Getmax(int Node,int L,int R,int gl,int gr){
if(L>R)return -1;
if(gl<=L&&R<=gr)return Seg2[Node];
int Mid=L+R>>1,ans=-1;
pushdown(Node);
if(Mid>=gl)ans=max(ans,Getmax(Node<<1,L,Mid,gl,gr));
if(Mid< gr)ans=max(ans,Getmax(Node<<1|1,Mid+1,R,gl,gr));
update(Node);
return ans;
}
void modify(int Node,int L,int R,int ml,int mr,int x){
if(ml<=L&&R<=mr){
lazy[Node]=x;
Seg[Node]=Seg2[Node]=x;
return ;
}
int Mid=L+R>>1;
pushdown(Node);
if(Mid>=ml)modify(Node<<1,L,Mid,ml,mr,x);
if(Mid< mr)modify(Node<<1|1,Mid+1,R,ml,mr,x);
update(Node);
}
int Find0(int x){
int L=x+1,R=Lim,ans=-1;
while(L<=R){
int Mid=L+R>>1;
if(!Getmin(1,1,Lim,L,Mid-1))R=Mid-1;
else if(!Get(1,1,Lim,Mid)){
ans=Mid;
break;
}
else L=Mid+1;
}
return ans;
}
int Find1(int x){
int L=x+1,R=Lim,ans=-1;
while(L<=R){
int Mid=L+R>>1;
if(Getmax(1,1,Lim,L,Mid-1)>0)R=Mid-1;
else if(Get(1,1,Lim,Mid)){
ans=Mid;
break;
}
else L=Mid+1;
}
return ans;
}
void Add(int x){
if(!Get(1,1,Lim,x))insert(1,1,Lim,x,1);
else{
int d=Find0(x);
insert(1,1,Lim,d,1);
modify(1,1,Lim,x,d-1,0);
}
}
void Del(int x){
if(Get(1,1,Lim,x))insert(1,1,Lim,x,0);
else{
int d=Find1(x);
insert(1,1,Lim,d,0);
modify(1,1,Lim,x,d-1,1);
}
}
int GetAns(int Node,int L,int R){
if(L==R)return L;
int Mid=L+R>>1;
pushdown(Node);
if(Seg2[Node<<1|1])return GetAns(Node<<1|1,Mid+1,R);
else return GetAns(Node<<1,L,Mid);
update(Node);
}
int main()
{
memset(lazy,-1,sizeof(lazy));
scanf("%d%d",&n,&q);
for(int i=1;i<=n;++i)scanf("%d",&a[i]);
for(int i=1;i<=n;++i){
Add(a[i]);
}
for(int i=1;i<=q;++i){
int x,y;scanf("%d%d",&x,&y);
Del(a[x]);
Add(a[x]=y);
printf("%d\n",GetAns(1,1,Lim));
}
}
