关于树性质维护的一类数据结构和算法（仍在更新中）
关于树性质维护的一类数据结构和算法（仍在更新中）

关于树性质维护的一类数据结构和算法（仍在更新中）

Ⅰ 树链剖分（轻重链剖分）

一、简介

树链剖分，计算机术语，指一种对树进行划分的算法，它先通过轻重边剖分将树分为多条链，保证每个点属于且只属于一条链，然后再通过数据结构（树状数组、SBT、Splay、线段树等）来维护每一条链。

这里主要讲的是轻重链剖分而并非长短链剖分。

二、前置姿势

  • LCA

  • DFS序

  • 线段树

三、基础概念

  • 重儿子：对于每一个非叶节点，它的子节点中子树节点最多的一个节点。

  • 轻儿子：对于每一个非叶节点，除了一个重儿子，其余均为轻儿子。

  • 重边：连接两个重儿子的边。

  • 轻边：除了重边的树边。

  • 重链：由一条重边连接而成的链。

四、树链剖分的核心思想

树链剖分的核心是将原树拆分为若干条轻重链，通过维护链上信息来保证树上信息维护的复杂度。

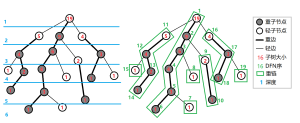
图出自OI-Wiki

五、算法流程-信息维护

考虑这样一道模板题：题目链接。

1. dfs1：处理出每个节点的深度、父节点、子树大小和重儿子

void dfs1(int x,int f,int deep){
    dep[x]=deep;//深度
    fa[x]=f;//父节点
    siz[x]=1;//维护子树大小
    int mxsiz=0;//最大的儿子的儿子数量（维护重儿子）
    for(int i=head[x];~i;i=nxt[i])if(to[i]^f){
        dfs1(to[i],x,deep+1);
        siz[x]+=siz[to[i]];
        if(mxsiz<siz[to[i]])mxsiz=siz[to[i]],hvson[x]=to[i];
    }
}

2. dfs2：按dfs序标号、处理出轻重链，Ltop表示链的顶端

void dfs2(int x,int Ltop){
    id[x]=++idcnt;
    na[idcnt]=a[x];
    top[x]=Ltop;
    if(!hvson[x])return ;
    dfs2(hvson[x],Ltop);
    for(int i=head[x];~i;i=nxt[i])if(to[i]^hvson[x]&&to[i]^fa[x]){
        dfs2(to[i],to[i]);
    }
}

tips：先处理重儿子，在处理轻儿子。

为什么？

因为这样对于一条重链上的重儿子id就是连续的，才可以用数据结构维护。

3. 将x到y路径+c

若x和y不在同一条链上，就将所在链的顶端深度较深的点修所在链修改。（id连续）

把x跳到x所在链顶端的那个点的上面一个点。

在同一条链上时直接修改。

void ModifyRoute(int x,int y,int c){
    while(top[x]^top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);//让x作为top深度更深的点
        ModifySection(1,1,n,id[top[x]],id[x],c);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    ModifySection(1,1,n,id[x],id[y],c);
}

4. 查询x到y的路径和

类似路径修改。

LL QueryRoute(int x,int y){
    LL res=0;
    while(top[x]^top[y]){//x、y不在一条链上
        if(dep[top[x]]<dep[top[y]])swap(x,y);//让x作为top深度更深的点
        (res+=QuerySection(1,1,n,id[top[x]],id[x]))%=P;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    (res+=QuerySection(1,1,n,id[x],id[y]))%=P;
    return res;
}

5. 子树修改

这个时候之前统计的子树大小就排上用场了。

子树内的id是连续的（dfs），所以直接用siz来整体修改即可。

void ModifySubtree(int x,int c){
    return (void)(ModifySection(1,1,n,id[x],id[x]+siz[x]-1,c));
}

6. 子树查询

类似子树修改。

LL QuerySubtree(int x){
    return QuerySection(1,1,n,id[x],id[x]+siz[x]-1);
}

7. 求LCA

不断向上跳重链，当跳到同一条重链上时，深度较小的结点即为 LCA。

向上跳重链时需要先跳所在重链顶端深度较大的那个。

int LCA(int x,int y){
    while(top[x]^top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        x=fa[top[x]];
    }
    return dep[x]>dep[y]?y:x;
}

总复杂度O(nlog2n)

源码链接

六、刷题题单

Ⅱ 树上启发式合并-DSU on Tree

一、简介

树上启发式合并，又称DSU on Tree，用来解决一些只涉及到子树信息维护的离线问题。

以较优的复杂度（暗示树上莫队）和较易理解的思想为人所知。

正如其名，其正是将子树信息从低到高合并来实现子树信息维护。

二、前置姿势

  • 树链剖分（轻重链）

三、算法流程

先给一个经典题，题目链接：

给出一棵n个节点的树，每个节点有一个对应颜色，求每个节点的子树内有多少种不同的颜色。n<=2e5

1. dfs1：处理出每个节点的深度、父节点、子树大小和重儿子

同树链剖分的dfs1。

多记录一个id代表的原节点

void dfs1(int x,int f){//处理出每个节点的父节点、子树大小和重儿子
    fa[x]=f,siz[x]=1,id[x]=++idcnt,rev[idcnt]=x;
    int mxsiz=0;
    for(int i=head[x];~i;i=nxt[i])if(to[i]^f){
        dfs1(to[i],x);
        siz[x]+=siz[to[i]];
        if(mxsiz<siz[to[i]])mxsiz=siz[to[i]],hvson[x]=to[i];
    }
}

2. dfs2：类似暴力的处理答案（核心）

树上启发式合并的核心思想就在于此。

基于重链剖分，对于当前节点的子节点，优先遍历轻儿子节点，计算其子树的信息后，不保留其对当前节点的贡献。

然后再遍历重儿子节点，保留其对子树答案的贡献。

然后再次遍历其他轻儿子节点，加入其贡献，得到当前节点答案。

void dfs2(int x,int fa,int Opt){
    //优先计算轻儿子的答案
    for(int i=head[x];~i;i=nxt[i])if(to[i]^fa&&to[i]^hvson[x]){
        dfs2(to[i],x,1);
    }
    if(hvson[x])dfs2(hvson[x],x,0);//计算重儿子答案
    for(int i=head[x];~i;i=nxt[i])if(to[i]^fa&&to[i]^hvson[x]){
        for(int j=id[to[i]];j<=id[to[i]]+siz[to[i]]-1;++j)Add(rev[j]);
    }//暴力统计子树信息，不统计重儿子信息是因为重儿子的信息会在子树内保留
    Add(x);
    Ans[x]=CntCol;
    if(Opt){//如果当前节点是轻儿子，就删除子树的贡献
        for(int i=id[x];i<=id[x]+siz[x]-1;++i)Del(rev[i]);
    }
}

源码链接

四、复杂度

O(nlogn)。

可以这么考虑：只有DFS到了轻儿子时，才会将轻儿子的贡献合并到上一级重儿子上。

树链剖分将树分割为不超过logn条重链，每个节点最多向上合并logn次。

所以整体复杂度O(nlogn)。

详细证明看OI-Wiki

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注